PDF-Download-Artikel – Vorschau:
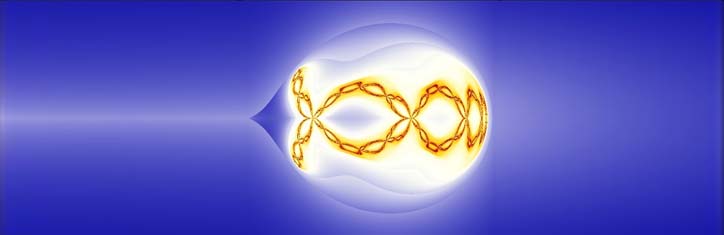
Fraktale Geometrie nach Benoît Mandelbrot gehört zu den faszinierendsten Gebieten der Mathematik. Ihre rekursiven Iterationen scheinen der Natur viel angemessener als die lineare, monokausale Vorgehensweise der Schulphysik. Die Dipl.-Physikerin Gabi Müller zeigt auf, dass die fraktale Mathematik die ideale Beschreibungsgrundlage für die Wirbelphysik darstellt. Es wird deutlich, wie sich das Lebendige seine Form erhalten kann. Hier spielt der mehrdimensionale Goldene Schnitt eine Rolle. Frappierend ist auch, dass bestimmte Körperformen wie Auge und Schädel als fraktale Muster auftauchen.
Nach Kauf und Zahlung steht der vollständige Artikel als PDF zum Download für Sie bereit:
– Bei Gastbestellung erhalten Sie den Download-Link per E-Mail mit der Bestellbestätigung.
– Als registrierter Kunde finden Sie den Download zusätzlich in Ihrem Kundenkonto (bis zu 10 Downloads möglich).
